Thinking about 0 to the power of 0
Half by accident I came across What is 0 to the power of 0? on Youtube, an inspiring recording of a normal high school class session about the value of$0^0$. Half way through the video I thought: It would be interesting to see a graph of $x^x$ when $x$ is getting closer to $0$.
With Python’s matplotlib (and seaborn on top) that’s pretty easy, so I plotted $f(x) = x^x$ for $x $:
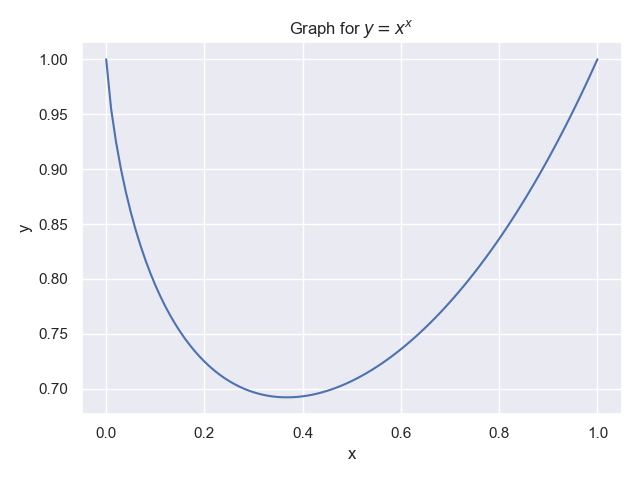
This graph suggests that for $x$ approaching $0$, $f(x)$ approaches $1$. But lets plot a bit closer to 0:
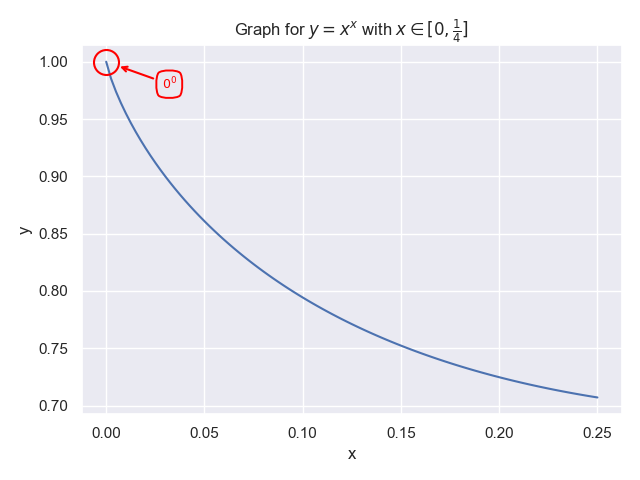
Same story. And if we look very close to $0$:
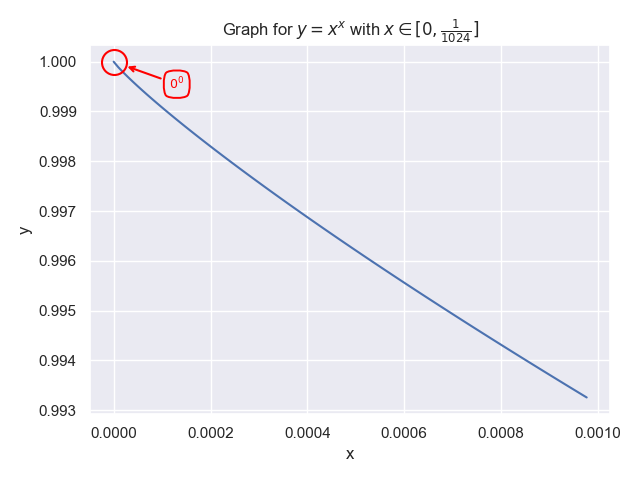
Same story again. So let’s propose:
$_{x ^+} x^x = 1$
From this it makes sense to set $x^x = 0$. This is indeed how many mathematicians1 (but not all of them2) define it. Actually a good overview of the issue is given on Wikipedia.
See for example Donald Benson, The Moment Of Proof: Mathematical Epiphanies, 1999, p.29: “The consensus is to use the definition $0^0 = 1$.”↩︎
See Charles Henry Edwards & David Penney, Calculus With Analytic Geometry, 1994, p.471: Although $a^0 = 1$ for any nonzero constant $a$, form $0^0$ is indeterminate[…]“↩︎